Mathematical representation of SVM
Mathematical representation of SVM
In the previous blog we have seen basics
of support vector machine.
In this blog we have to see maths
intuition behind the support vector machine.
The most important in case of SVM is creat
hyperplane and calculate marginal distance between positive hyperplane and
negative hyperplane, so that it is easy to classify data.
First step is to calculate or marginal
distance between +ve hyperplane and – ve
hyperplane.
Consider following example.
Ex. Suppose their are two points (-5,0) & (5,5).
Hear
slope = -1 Therefore m = -1and & b
= 0, As line passes through origin
Putting it in equation 2 we get
Any point left to the line is always -ve
For point ( 5, 5) value of y is calculated as
Thus straight line will divide the data. Points
above the line is in one group and points below the line is in another group.
For SVM Only straight line is
not sufficient we need to calculate Hyperplane
Fig 2 shows hyperplane (middle blue line) and margin middle (two dotted
lines)
Disance between dotted blue lines is a marginal distance
One red square and two green dots which
are on dotted lines are Support vectors
If b represents intersection of line on x axis then equation of blue line is
Training tuples are 2D, (X =(x1,
x2) where x1 and x2
are attributes of A1and A2)
Considering w0 as the
additional weight . and rewriting Equation (5) as
w0+ w1x1+
w2x2 = 0 -----------------------6
Any point that lies above the
hyperplane satisfies the following equation
w0+
w1x1+ w2x2 > 0 ----------------------7
Any point that lies below the
hyperplane satisfies the following equation
w0+
w1x1+ w2x2 > 0 ----------------------8
Adjusting the weight and
hyperplanes define the sides of the margin can be written as
H1
: w0+ w1x1+ w2x2 ≥
1 for yi = +1
---------------9
H2
: w0+ w1x1+ w2x2 ≤
-1 for yi = -1
-------------------10
From the above two equation (9) and
(10) we can say that,any tuple that falls on or above H1 belongs to class +1 and any tuple that
falls on or bellow H2 belongs to class -1
Combine two equations (5) and (6)
get
Yi (w0+ w1x1+ w2x2) ≥ 1
,
Any Training tuples that fall on
hyperplanes H1 or H2
(i.e.,the “sides” defining the
margin)satisfy Eq.(11) and are called support vectors .That is. They are equally
close to the (separating) Hyperplane
The distance from the separating
hyperplane to ant point on H1 is
1/
Multiple choice questions for SVM
Q1. SVM
is ----------type of learning(Supervised)
Q2
SVM is used to solve -----------Type
of problems.(Clssification and Regression)
Q3
In SVM decision boundaries which
classify the data is called ---------(hyperplane)
Q4 SVM is used for --------type of data(linearly
seperable and non linearly seperable)
Q5 Support vector machine is used for----
(single diamensinal and multidimensional data)
Q6 In SVM equation of line ------to separate
the data
Q7 In SVM equation of plane ------to separate the data
Q8 ---- are
used to make non-separable data into separable data in non linear classifier.(Kernel)
Q9 ----- map data from low dimensional space to high dimensional
space forSVM
classification.r(kernel)
Q10 In SVM Hyperplane must have ----margin(high)
Q11 Equation of hyperplane is ---
Q12 Equation of hyperplane margin is---
Q13 Support vectors are the points which lies on---(boundary of the
hyperplane)
Q14) SVM is used for ---------type of data(Structured and unstructured)
Q15 ----------------- is the real strength of svm(




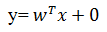










Comments
Post a Comment